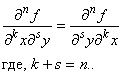Дифференцирование сложной функции.

Теорема: Пусть  и функции x = x(u, v)Î, y(u, v)Î = x(u₀, v₀), y₀ = y(u₀, v₀).

Тогда f(x(u, v), y(u, v))ÎD(u₀, v₀) и

Доказательство: Рассмотрим разности:

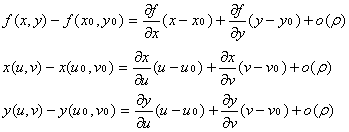
из которых следует, что

f(x(u, v), y(u, v)) - f(x(u₀, v₀), y(u₀, v₀)) =

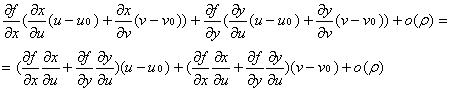
Следовательно, по определению дифференцируемости функция двух переменных:

f(x(u, v), y(u, v))ÎD(u₀, v₀) и

Теорема доказана.

Дифференциал функции двух переменных. Свойство инвариантности дифференциала.

Пусть .

Определение: Дифференциал d функции  в точке  называется следующее выражение:

или сокращённо: , где dx и dy – дифференциалы переменных x и y.

Пусть x = x(u, v)Î и y(u, v)Î.

Тогда по определению:

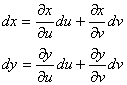
Следовательно, мы можем представить df в следующем виде:

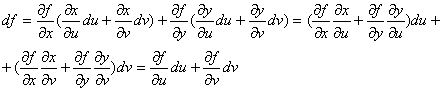
Последнее равенство следует из доказанных формул замены переменных.

Таким образом df можно представить в виде:

Это равенство и выражает свойство инвариантности первого дифференциала.

Частные производные высших порядков. Равенство вторых смешанных производных.

Первые частные производные  и  есть функции от переменных x и y. Назовём по определению вторыми частными производными функции  следующие выражения:

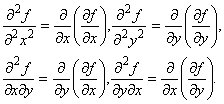
Пример:

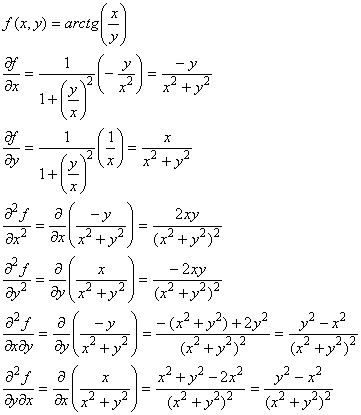
Заметим, что =. Это свойство обобщается следующей теоремой.

 Теорема: Пусть ,  и  непрерывны в некоторой окрестности точки (x, y), а  и  непрерывны в самой точке (x, y). Тогда в точке (x, y) равенство:

=

Доказательство: Рассмотрим вспомогательную функцию

.

Обозначим

Заметим, что

.

По формуле Лагранжа:

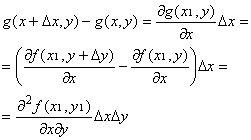
где x₁Î(x, x + Δx), y₁Î(y, y + Δy).

Аналогично, для функции h(x, y) справедливы равенства:

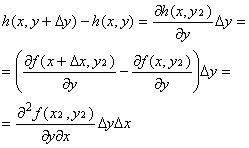
где x₂Î(x, x + Δx) и y₂Î(y, y + Δy).

Из доказанных равенств следует, что

 

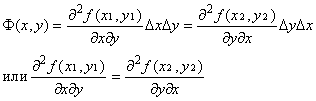
Если

Поэтому, ввиду непрерывности функций  и  в точке (x, y) справедливо равенство: =

Теорема доказана.

Следствие:

Для смешанных производных высших порядков верно равенство: